Stable Matching Algorithms (Stable marriage problem)

Stable Matching Algorithms

Specification

Input: 'n명의 남자와 'n'명의 여자가 있으며, 모든 남녀들에게는 다른 성별에 대한 선호도의 순서가 있다.

n개의 원소가 있는 배열이며, 각각의 원소에는 각각의 남자와 여자 = 1, ..., n까지에 대한 선호도 순서이다.

Output: Stable perfect Matching

두개의 n개의 원소 배열이며, wife[m] = w와 husband[w] = m과 같이 매칭되어 있고, 값이 0일 경우에는 매칭되지 않았다는 뜻이다.

Definition: Tuple (w, m`)이 unstable하다는 것은, w가 만약 현재 매칭된 m보다 m`을 더 선호하고, m`이 현재 매칭된 w`보다 w를 선호할 경우, unstable하다고 한다.

즉, 남자와 여자가 현재 각각 매칭되어 있는 상대보다 서로의 선호도가 더 높음에도 불구하고 매칭이 되지 않을 경우를 unstable되었다고 말한다.

Algorithm

Gale-Shapley (1962)

M := {}

WHILE 어떤 남자 m이 매칭되지 않았을 경우
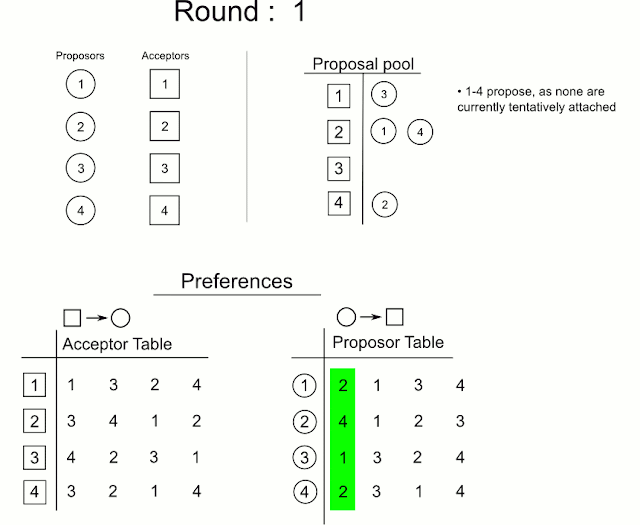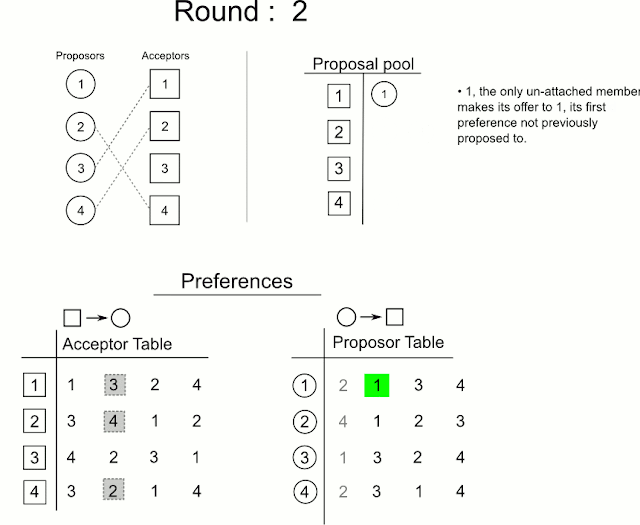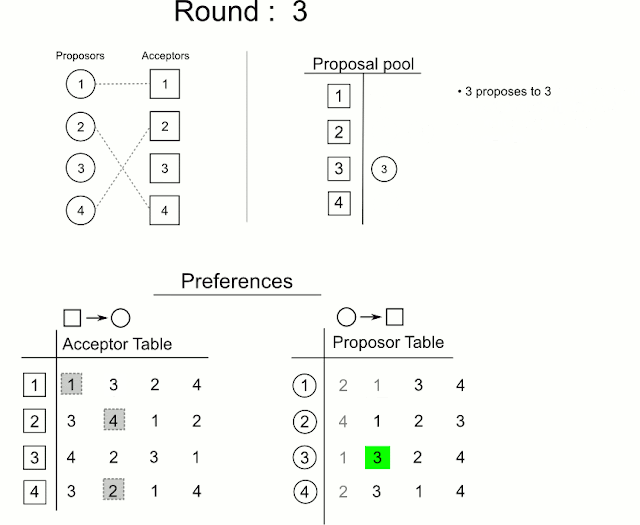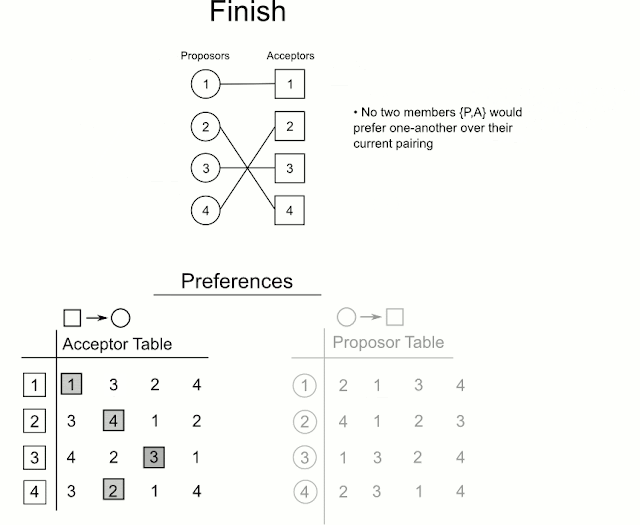
  남자 m이 아직 프로포즈하지 않은 여자들 중, 가장 선호도가 높은 여자 w에 대해 프로포즈한다.
  
   IF 만약 w가 매칭되지 않은 상태라면, M에 tuple (m, w)를 추가한다.

   ELIF 만약 w가 현재 매칭되어 있는 상대인 m`보다 m을 선호한다면, M에 있는 tuple (m`, w)를 tuple (m,w)로 바꾼다.

  ELSE w는 m의 프로포즈를 거절한다.

ENDWHILE

Proof of Correctness: Stability

Contradiction을 이용하여 증명해보자.

Pf) (by Contradiction)
남자 A와 여자 B에 대해 A-B pair가 unstable하다고 가정해보자. A와 B는 Gale-Shapley matching S*에서 서로의 현재 매칭된 파트너보다 서로를 더 선호한다고 해보자.
즉 S*에서 (A, A*), (B*, B)에 대해서, A는 A*보다 B를 선호하고, B는 B*보다 A를 선호한다고 가정하자.

그렇다면 이것이 이러한 현상이 어떻게 일어날 수 있는가?

1) A가 B에게 프로포즈를 하지 않은 경우
2) A가 B에게 프로포즈를 했으나 거절당한 경우

두 가지로 나눌 수 있다.

Case 1)을 살펴보면 A는 S*의 파트너 A*보다 B를 선호한다.
Gale-Shapley Matching 알고리즘에 의해 A는 A*보다 B에게 먼저 프로포즈를 해야한다.
그러므로 Unstable하지 않는다.

Case 2)를 살펴보자. A는 B에게 프로포즈를 하였다.
B는 A를 거절하였다.
하지만 A는 A*보다 B를 더 선호한다.
그러므로 unstable하지 않는다.

즉, Contradiction에 의해 A-B pair는 unstable한 pair가 아니다.

Code


 

def stable_matching(M, W):
    M_list = [0] * (len(M)+1)
    W_list = [0] * (len(W)+1)
    M_candidate = [0] * (len(M)+1)
    #W_candidate = [0] * (len(W)+1)
    #M_preference = [0] * (len(M)+1)
    W_preference = [0] * (len(W)+1)
    
    #for i in range(0, len(M_preference)-1):
    #    temp = [0] * len(M)
    #    for j in range(0, len(M[i])):
    #        temp[M[i][j]-1] = j
    #    M_preference[i+1] = temp
    
    for i in range(0, len(W_preference)-1):
        temp = [0] * len(W)
        for j in range(0, len(W[i])):
            temp[W[i][j]-1] = j
        W_preference[i+1] = temp
    
    #print(M_preference)
    #print(W_preference)
    #print(M_candidate)
    #print(W_candidate)
    
    
    def check_no_marriage(L):
        bool_check = 0
        for i in range(1, len(L)):
            if L[i] == 0:
                bool_check = 1
                break;
        return bool_check
    
    while check_no_marriage(M_list) or check_no_marriage(W_list):
        for i in range(1, len(M_list)):
            if M_list[i] != 0:
                continue
            m = i
            target_w = M[m-1][M_candidate[m]]
            #print("target man ", m)
            #print("target woman ", target_w)


            if W_list[ target_w ] == 0:
                M_list[m] = target_w
                W_list[target_w] = m
            
            else:
                if W_preference[target_w][m-1] < W_preference[target_w][W_list[target_w]-1]:
                    M_list[W_list[target_w]] = 0
                    M_candidate[W_list[target_w]] += 1
                    M_list[m] = target_w
                    W_list[target_w] = m
                else:
                    M_candidate[m] += 1
            #print("M_list ", M_list)
            #print("W_list ", W_list)
            
    #print(M_list)
    #print(W_list)
    
    results = list()
    for i in range(1, len(M_list)):
        results.append( (i,M_list[i]) )
    
    return results