Introduction to Deep Learning - (2)
지난 시간에 머신러닝과 딥러닝 정의에 대해서 배워보는 시간을 가졌다.
머신러닝은 주어진 데이터 x에 대해서 어떠한 결과가 나올지에 대한 과정이나 가설을 스스로 학습하는 분야라 했다.
그렇다면 주어진 데이터 x에 대해서 학습한다는 이야기는, 학습용 데이터가 따로 있으며, 기계가 잘 학습했는지에 대해 확인하기 위한 확인 데이터가 따로 필요하다는 것을 의미한다.
학습용 데이터를 Training Data라 부르며, 확인용 데이터를 Test Data라 부른다.
기계가 가지고 있는 가설 h(x)에 대하여, Training Data를 통해 잘 예측할 수 있도록 h(x)를 수정하고 최종적으로 Test Data를 통해 잘 예측이 되는지 확인하는 것이다.
Training Data와 Test Data에는 서로간 겹치는 데이터가 존재하지 않아야한다. 만약 미리 학습을 했던 Data가 Test Data에 들어갈 경우, 해당 Data에 대해서 항상 옳은 값을 내놓을 확률이 매우 높다. 우리는 이 기계가 잘 학습했는지를 알고 싶기 때문에 항상 옳은 값을 내놓을 데이터로 테스트를 할 이유가 전혀 없다. 옳은 값을 내놓을지, 틀린 값을 내놓을지 모를 구분되는 테스트 데이터로 테스트를 해야 균형있게 가설을 검증해볼 수 있을 것이다.
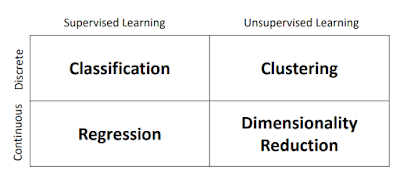
머신 러닝 문제들은 다음과 같은 카테고리로 나누어질 수 있다.
먼저 우리가 학습하려고 하는 데이터가 정수와 같은 Discrete한 정보의 해답을 예측하려고 하는가, 아니면 학습하려고 하는 데이터가 연속적인 값을 예측하려고 하는가에 대해서 나눌 수 있다.
예를 들어서 내가 가지고 있는 데이터를 통해서 이 데이터가 새인지, 강아지인지, 고양이인지 알아보려고 한다면, 이러한 예측하려는 정보들은 모두 이산적인 정보로 나타낼 수 있다. 예를 들면, 새는 1, 강아지는 2, 고양이는 3과 같은 특정 숫자들로 assign하여 예측할 수 있다.
연속적인 값을 예측하는 것은, 예를 들어 바둑을 진행할 때, 내가 지금 이 상대에게 이길 수 있는 확률과 같은 값을 예측하는 것을 생각할 수 있다.
또 다른 카테고리는 Supervised / Unsupervised가 있다.
우리가 학습하려는 데이터가 이미 정답 정보를 가지고 있는가, 즉 label을 가지고 있는가로 분류되는데, 정답 정보를 가지고 있는 경우 이를 Supervised Learning이라 하며, 정답 정보가 없는 경우에 Unsupervised라고 한다.
Supervised Learning과 같은 경우에는 다음과 같은 그림을 보면 이해하기 쉬울 것이다.
-Supervised Learning
반면, Unsupervised Learning같은 경우에는 정답 정보가 없다. 하지만 Data내에서 분류나 회귀가 될 수 있는 정보들을 f(x)를 통하여 직접 분류/회귀한다.
그럼 이제 각각의 카테고리들을 살펴보도록 하자.
-Regression : 연속적인 실수값을 예측하기 위해 training data에 예측 함수 f(x)를 fitting 시키는 것.
-Clustering : 자동적으로 instance들을 그룹화한다. 이러한 그룹화는 같은 그룹내에의 instance들이 다른 group의 instance보다 유사하도록 진행한다.
-Dimensionality Reduction : Input data의 dimension을 줄이는 것.
그 외에, Semi-supervised Learning이라고 label된 데이터와 unlabel된 데이터 모두를 가지고 model을 training하는 learning method도 존재한다.
-------------------------------------------------------------------------------------
그렇다면, 기계는 과연 어떤 식으로 model을 학습하여야 하는가?
기계가 가지고 있는 model은 예측된 값과 실제 정답을 비교한 Loss function을 최소화하는 방향으로 학습하면서 model을 서서히 fitting한다.
예를 들어 음수가 아니고, 실수값을 가지고 있는 Loss function $L(\hat{y},y)$의 값을 줄이는 것인데, 새로운 data (x,y)에 대하여 가설 h에 관한 true risk R은 다음과 같이 정의된다.
$$R(h) = E[L(h(x),y)] = \int L(h(x).y)dP(x,y) $$
이는 Generalization error라고도 알려져 있다.
머신 러닝의 목표는 유한한 set H에 대하여 다음을 만족하는 h*를 찾는 것이다.
$$ h* = argmin_{h\in H} R(h) $$
하지만 P(x,y)가 어떠한 분포를 갖고 있는지 모르기 때문에 R(h)는 실제로 계산될 수 없다.
그렇기 때문에 우리는 Empirical risk를 최소화하려고 한다. Empirical risk는 true risk와 유사한 함수이다.
$$R_{emp}(h) = \frac{1}{m}\sum^{m}_{i=1} L(h(x_i),y_i) $$
$$\hat{h} = argmin_{h\in H} R_{emp}(h) $$
regression과 같은 예시일 경우, 우리는 average squared loss를 사용한다.
$$L(h(x_i),y_i) = (h(x_i)-y_i)^2 $$
하지만, 이러한 model을 만드는 것은 test data에서 좋은 정확도를 보여줄 것이라는 것을 보장하지 못한다. 왜냐하면 training data set에서만 좋은 정확도를 보여주도록 training data에 대하여서만 optimization되었기 때문이다.
다음과 같은 두 개의 그래프를 살펴보자.
Red dot은 주어진 sample data이다.
Green curve는 true function을 나타낸 그래프이며, Blue curve는 prediction으로 유추된 curve이며, 위와 같은 그래프 경우에는 smooth하고 아래와 같은 그래프 같은 경우에는 굉장히 터프한 것을 볼 수 있다.
prediction curve를 볼 경우 굉장히 터프한데도 불구하고 그 empirical risk가 0에 해당하는 것을 볼 수 있다.
다음과 같은 노란색 new data가 주어질 경우 해당하는 loss가 blue curve 관점에서 보면 굉장히 크다는 것을 알 수 있다.
이와 같이 training data에 국한되어 그래프가 fitting되어 test data 예측값의 정확도가 낮을 경우 overfitting이라 부른다.
이러한 문제는 굉장히 높은 차원에서 polynomial function을 fitting했기에 일어난 결과일 수도 있다. 복잡한 모델 같은 경우에는 그래프의 높낮이의 편차가 매우 극심한 것을 알 수 있다.
그렇기 때문에 머신 러닝 알고리즘은 다음과 같은 두 가지의 목적을 잘 해결해야한다.
1. training error, 즉 empirical risk를 최소화해야한다.
2. 하지만 training과 test error의 차이를 줄여야한다.
이러한 두 가지 중요한 목적에 상응하는 두 가지 factor가 존재한다 : Underfitting과 Overfitting.
Underfitting은 training set의 값을 충분히 학습하지 못하여 model이 training data에서 배운 학습 내용을 잘 반영하지 못한 것을 뜻하고,
Overfitting은 training set의 값을 과하게 반영하여 training set에 편향되게 정확도가 좋고, 이외의 data에서는 결과값이 좋지 못한 경우를 말한다.
우리는 이러한 model이 overfitting인지 underfitting인지 그것의 capacity를 변경하는 것으로 조정할 수 있다.
학습 알고리즘의 capacity를 조정하는 방법 중 하나는 바로 가설 공간을 선택하는 것이다.
아까 직전의 regression problem을 떠올려보자. 즉 위의 그림을 보자. 아까 나타낸 문제점은 너무나 높은 차수의 function으로 fitting하려 했기 때문에 발생한 문제였다. 이러한 문제점은 간단히 function의 degree를 조정하는 것으로 더 좋은 방향으로 수정할 수 있다.
이러한 model의 capacity를 수정하는 것으로 더 좋은 결과를 볼 수 있는 예시를 살펴보자.
그림을 살펴보면, 당연히 차수가 낮게되면 해당 training data를 충분히 반영하지 못한 점이 있다. 하지만 차수가 너무 높게되면 training data에 너무 편향적으로 학습하게 되어 test data에서의 error가 커지게 된다. 만약 적정선의 degree를 찾게 된다면, test data에서도, training data에서도 error를 줄일 수 있게 된다. (여기서 말하는 error란 loss function을 의미한다.)
------------------------------------------------------------------------------------------
다음 자에서는 Estimation에 대한 내용을 포스팅하려한다.
*해당 내용들은 모두 2018년도 봄학기 KAIST, 딥러닝 특강 강의를 토대로 작성하였습니다.
머신러닝은 주어진 데이터 x에 대해서 어떠한 결과가 나올지에 대한 과정이나 가설을 스스로 학습하는 분야라 했다.
그렇다면 주어진 데이터 x에 대해서 학습한다는 이야기는, 학습용 데이터가 따로 있으며, 기계가 잘 학습했는지에 대해 확인하기 위한 확인 데이터가 따로 필요하다는 것을 의미한다.
학습용 데이터를 Training Data라 부르며, 확인용 데이터를 Test Data라 부른다.
기계가 가지고 있는 가설 h(x)에 대하여, Training Data를 통해 잘 예측할 수 있도록 h(x)를 수정하고 최종적으로 Test Data를 통해 잘 예측이 되는지 확인하는 것이다.
Training Data와 Test Data에는 서로간 겹치는 데이터가 존재하지 않아야한다. 만약 미리 학습을 했던 Data가 Test Data에 들어갈 경우, 해당 Data에 대해서 항상 옳은 값을 내놓을 확률이 매우 높다. 우리는 이 기계가 잘 학습했는지를 알고 싶기 때문에 항상 옳은 값을 내놓을 데이터로 테스트를 할 이유가 전혀 없다. 옳은 값을 내놓을지, 틀린 값을 내놓을지 모를 구분되는 테스트 데이터로 테스트를 해야 균형있게 가설을 검증해볼 수 있을 것이다.
머신 러닝 문제들은 다음과 같은 카테고리로 나누어질 수 있다.
먼저 우리가 학습하려고 하는 데이터가 정수와 같은 Discrete한 정보의 해답을 예측하려고 하는가, 아니면 학습하려고 하는 데이터가 연속적인 값을 예측하려고 하는가에 대해서 나눌 수 있다.
예를 들어서 내가 가지고 있는 데이터를 통해서 이 데이터가 새인지, 강아지인지, 고양이인지 알아보려고 한다면, 이러한 예측하려는 정보들은 모두 이산적인 정보로 나타낼 수 있다. 예를 들면, 새는 1, 강아지는 2, 고양이는 3과 같은 특정 숫자들로 assign하여 예측할 수 있다.
연속적인 값을 예측하는 것은, 예를 들어 바둑을 진행할 때, 내가 지금 이 상대에게 이길 수 있는 확률과 같은 값을 예측하는 것을 생각할 수 있다.
또 다른 카테고리는 Supervised / Unsupervised가 있다.
우리가 학습하려는 데이터가 이미 정답 정보를 가지고 있는가, 즉 label을 가지고 있는가로 분류되는데, 정답 정보를 가지고 있는 경우 이를 Supervised Learning이라 하며, 정답 정보가 없는 경우에 Unsupervised라고 한다.
Supervised Learning과 같은 경우에는 다음과 같은 그림을 보면 이해하기 쉬울 것이다.
-Supervised Learning
이미 이미지에 Hamburger라는 정답 정보를 가지고 있는 Training data를 통해 Hamburger로 분류되기 위한 f(x)를 학습시킨다.
-Unsupervised Learning
그럼 이제 각각의 카테고리들을 살펴보도록 하자.
-Regression : 연속적인 실수값을 예측하기 위해 training data에 예측 함수 f(x)를 fitting 시키는 것.
-Classification : 새로운 Instance가 어떠한 category에 해당할지 예측하는 것.
-Clustering : 자동적으로 instance들을 그룹화한다. 이러한 그룹화는 같은 그룹내에의 instance들이 다른 group의 instance보다 유사하도록 진행한다.
-Dimensionality Reduction : Input data의 dimension을 줄이는 것.
그 외에, Semi-supervised Learning이라고 label된 데이터와 unlabel된 데이터 모두를 가지고 model을 training하는 learning method도 존재한다.
-------------------------------------------------------------------------------------
그렇다면, 기계는 과연 어떤 식으로 model을 학습하여야 하는가?
기계가 가지고 있는 model은 예측된 값과 실제 정답을 비교한 Loss function을 최소화하는 방향으로 학습하면서 model을 서서히 fitting한다.
예를 들어 음수가 아니고, 실수값을 가지고 있는 Loss function $L(\hat{y},y)$의 값을 줄이는 것인데, 새로운 data (x,y)에 대하여 가설 h에 관한 true risk R은 다음과 같이 정의된다.
$$R(h) = E[L(h(x),y)] = \int L(h(x).y)dP(x,y) $$
이는 Generalization error라고도 알려져 있다.
머신 러닝의 목표는 유한한 set H에 대하여 다음을 만족하는 h*를 찾는 것이다.
$$ h* = argmin_{h\in H} R(h) $$
하지만 P(x,y)가 어떠한 분포를 갖고 있는지 모르기 때문에 R(h)는 실제로 계산될 수 없다.
그렇기 때문에 우리는 Empirical risk를 최소화하려고 한다. Empirical risk는 true risk와 유사한 함수이다.
$$R_{emp}(h) = \frac{1}{m}\sum^{m}_{i=1} L(h(x_i),y_i) $$
$$\hat{h} = argmin_{h\in H} R_{emp}(h) $$
regression과 같은 예시일 경우, 우리는 average squared loss를 사용한다.
$$L(h(x_i),y_i) = (h(x_i)-y_i)^2 $$
하지만, 이러한 model을 만드는 것은 test data에서 좋은 정확도를 보여줄 것이라는 것을 보장하지 못한다. 왜냐하면 training data set에서만 좋은 정확도를 보여주도록 training data에 대하여서만 optimization되었기 때문이다.
다음과 같은 두 개의 그래프를 살펴보자.
Red dot은 주어진 sample data이다.
Green curve는 true function을 나타낸 그래프이며, Blue curve는 prediction으로 유추된 curve이며, 위와 같은 그래프 경우에는 smooth하고 아래와 같은 그래프 같은 경우에는 굉장히 터프한 것을 볼 수 있다.
prediction curve를 볼 경우 굉장히 터프한데도 불구하고 그 empirical risk가 0에 해당하는 것을 볼 수 있다.
이와 같이 training data에 국한되어 그래프가 fitting되어 test data 예측값의 정확도가 낮을 경우 overfitting이라 부른다.
이러한 문제는 굉장히 높은 차원에서 polynomial function을 fitting했기에 일어난 결과일 수도 있다. 복잡한 모델 같은 경우에는 그래프의 높낮이의 편차가 매우 극심한 것을 알 수 있다.
그렇기 때문에 머신 러닝 알고리즘은 다음과 같은 두 가지의 목적을 잘 해결해야한다.
1. training error, 즉 empirical risk를 최소화해야한다.
2. 하지만 training과 test error의 차이를 줄여야한다.
이러한 두 가지 중요한 목적에 상응하는 두 가지 factor가 존재한다 : Underfitting과 Overfitting.
Underfitting은 training set의 값을 충분히 학습하지 못하여 model이 training data에서 배운 학습 내용을 잘 반영하지 못한 것을 뜻하고,
Overfitting은 training set의 값을 과하게 반영하여 training set에 편향되게 정확도가 좋고, 이외의 data에서는 결과값이 좋지 못한 경우를 말한다.
우리는 이러한 model이 overfitting인지 underfitting인지 그것의 capacity를 변경하는 것으로 조정할 수 있다.
학습 알고리즘의 capacity를 조정하는 방법 중 하나는 바로 가설 공간을 선택하는 것이다.
아까 직전의 regression problem을 떠올려보자. 즉 위의 그림을 보자. 아까 나타낸 문제점은 너무나 높은 차수의 function으로 fitting하려 했기 때문에 발생한 문제였다. 이러한 문제점은 간단히 function의 degree를 조정하는 것으로 더 좋은 방향으로 수정할 수 있다.
이러한 model의 capacity를 수정하는 것으로 더 좋은 결과를 볼 수 있는 예시를 살펴보자.
그림을 살펴보면, 당연히 차수가 낮게되면 해당 training data를 충분히 반영하지 못한 점이 있다. 하지만 차수가 너무 높게되면 training data에 너무 편향적으로 학습하게 되어 test data에서의 error가 커지게 된다. 만약 적정선의 degree를 찾게 된다면, test data에서도, training data에서도 error를 줄일 수 있게 된다. (여기서 말하는 error란 loss function을 의미한다.)
------------------------------------------------------------------------------------------
다음 자에서는 Estimation에 대한 내용을 포스팅하려한다.
*해당 내용들은 모두 2018년도 봄학기 KAIST, 딥러닝 특강 강의를 토대로 작성하였습니다.
댓글
댓글 쓰기