Introduction to Deep Learning - (3)
Estimators, Bias and Variance
Point Estimation
Point estimation은 우리가 관심있는 것들에 대한 단일 최고의 예측을 제공하려는 시도 중에 하나이다.
예를 들어서, ${x^{(1)}, ... , x^{(m)}}$이 data point $m$개의 세트라고 하면, 포인트 추정자(point estimator)는 data에 관한 어느 함수로 정의된다:
$$ \hat{\theta_m} = h(x^{(1)}, ... , x^{(m)}). $$
물론 이러한 정의에서는 $h$ 함수 자체가 참 $\theta$값에 가까운 값을 요구하지도 않기 때문에 어느 함수라도 추정자로서 적합하지만, 물론 좋은 추정자는 참 $\theta$값을 생성하는 함수이겠다.
그렇다면, 통계적 관점을 집어넣는다면 어떻게 될까.
먼저 앞에서 언급한 부분을 생각하면, 실제 매개 변수 값 $\theta$는 고정되어 있지만 우리가 모르는 값이며, 점 추정치(point estimate) $\theta$는 데이터의 함수이다.
Data가 무작위적 과정을 거쳐 뽑아나왔고, data의 함수도 무작위이기 때문에 $\hat{\theta}$도 무작위적 과정이다.
점 추정은 또한 input과 target variable의 추정을 참조하기도 한다.
우리는 함수 추정자로써 점 추정의 이러한 형태들을 취하기도 한다.
Function Estimation
주어진 input vector x에 대하여 변수 y를 예측한다고 상상하자.
우리는 y와 x에 관한 대략적인 관계를 묘사하는 참 함수 $f(x)$가 존재한다고 가정한다.
(e.g.) 우리는 $y = f(x) + \epsilon$과 같은 식을 상상할 수 있고, 이 때 $\epsilon$은 x로부터 예측되지 않은 y의 부분값이다.
함수 추정에서 우리는 추정자 h에 대해 f를 근사시키고 싶어한다.
Bias
추정자의 Bias는 다음과 같이 정의된다.
$$bias(\hat{\theta}_m) = E(\hat{\theta}_m) - \theta$$
이 때, $\theta$는 데이터 생성 분포를 정의하는 데 사용되는 $\theta$의 실제 기본값이다.
만약 $bias(\hat{\theta}_m)=0$이면, $E((\hat{\theta}_m)) = \theta$이므로, 추정치$\hat{\theta}_m$가 비편향 (unbiased)됐다고 하며,
만약 $\lim_{m->\infty}bias(\hat{\theta}_m)=0$일 경우, $\lim_{m->\infty}E(\hat{\theta}_m) = \theta$이므로 $\hat{\theta}_m$가 asymptotically unbiased됐다고 한다.
이러한 식으로보면 잘 이해가 안 되니까 예시를 들어서 살펴보도록 하자.
먼저 data sample $\{x^{(1)}, ... x^{(m)}\}$에 대해 모두 독립적이고 이상적으로 베르누어 분포를 따른다고하자. 즉 data sample들이 Bernoulli distribution으로부터 비롯됐다고 가정하자. 이 때, 평균을 $\theta$라 하면,
$$P(x^{(i)};\theta) = \theta^{x^{(i)}}(1-\theta)^{(1-x^{(i)})}$$
분포 \theta 파라미터에 대한 일반적인 추정치는 training sample의 평균이다:
$$\hat{\theta}_m = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$
그렇다면 이러한 추정치가 편향되어 있는지 편향되지 않았는지 확인해보자.
$$ bias(\hat{\theta}_m) = E[\hat{\theta}_m] - \theta $$
$$ = E[\frac{1}{m}\sum^m_{i=1} x^{(i)}] - \theta = \frac{1}{m}\sum^m_{i=1}E[x^{(i)}] - \theta $$
$$ = \frac{1}{m}\sum^m_{i=1}\sum^1_{x^{(i)}=0}(x^{(i)}\theta^{x^{(i)}}(1-\theta)^{(1-x^{(i)})}) - \theta $$
$$ = \frac{1}{m}\sum^m_{i=1}(\theta) - \theta = \theta - \theta = 0 $$
따라서 $$\hat{\theta}_m = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$는 편향되지 않았다.
그렇다면 편향되어있는 추정치의 예시에는 뭐가 있을까.
Gaussian distribution의 Variance parameter $\sigma^2$에 대해 생각해보자.
샘플 Variance는 하나의 추정치로써 다음과 같이 정의될 수 있다:
$$\hat{\sigma}^2_m = \frac{1}{m}\sum^m_{i=1}(x^{(i)} - \hat{\mu}_m)^2$$
그럴 경우, 이 추정치의 bias는
$$ bias(\hat{\sigma}^2_m) = E[\hat{\sigma}^2_m] - \sigma^2 = E[\frac{1}{m}\sum^m_{i=1}(x^{(i)}- \hat{\mu}_m)^2] - \sigma^2 = \frac{m-1}{m}\sigma^2 - \sigma^2 = - \frac{\sigma^2}{m} $$
따라서 sample variance는 편향적이다.
정리해보면 Discrepancy들은 다음과 같다.
Bias
$$ Bias[h(x)] = \bar{h(x)} - f(x) $$
Variance
$$ Var[h(x)] = E_p[(h(x)-\bar{h(x)})^2] $$
Noise
$$ Noise[h(x)] = E[(y-f(x))^2] = E[\epsilon^2] = \sigma^2 $$
Bias-Variance Decomposition
우리는 variance lemma을 통해 기대되는 예측 에러값을 분해할 수 있다.
$$E[(y-h(x))^2] = E[h(x)^2 - 2yh(x) + y^2] = E[h(x)^2] + E[y^2] - 2E[y]E[h(x)]$$
x에 대한 가설의 평균 예측을 $\bar{h(x)} = E[h(x)]$라 하자.
첫 번째 term은 variance lemma $E[X^2] = Var[X] + bar{X}^2$에 의해 다음과 같이 분해될 수 있다.
$$E[h(x)^2] = E[(h(x)-\bar{h(x)})^2] + \bar{h(x)}^2$$
두 번째 term은 다음과 같이 분해될 수 있다.
$$E[y^2] = E[(y-f(x))^2] + f(x)^2$$
그렇다면 이러한 식을 한꺼번에 모아두자.
$$E[(y-h(x))^2]$$
$$=E[h(x)^2-2yh(x)+y^2] $$
$$=E[h(x)^2]+E[y^2]-2E[y]E[h(x)]$$
$$=E[(h(x)-\bar{h(x)})^2] + \bar{h(x)}^2 + E[(y-f(x))^2] + f(x)^2 - 2f(x)\bar{h(x)} $$
$$=E[(h(x)-\bar{h(x)})^2] + (\bar{h(x)}-f(x))^2 + E[(y-f(x))^2] $$
$$=Var + Bias^2 + Noise $$
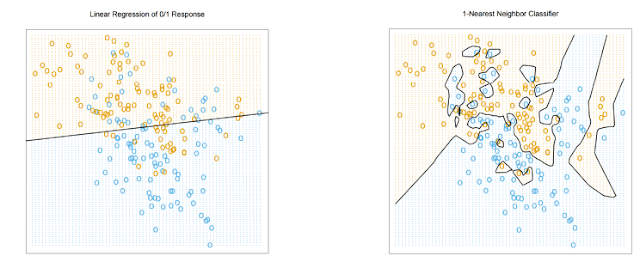
위와 같은 그림에서 왼쪽 그림은 높은 Bias를 가지고 있지만 낮은 Variance를 가지고 있다, 하지만 오른쪽 그림에서는 낮은 Bias를 가지고 있지만 높은 Variance를 가지고 있다.
우리는 그림과 같이 Bias와 Variance 모두가 적절하게 낮은 Optimal Capacity를 찾는 것이 목표이다.
Linear Regression
우리는 집의 가격과 그 집의 넓이에 관한 데이터를 가지고 있다고 생각하자.
우리는 이러한 데이터 포인트들에 대하여 직선 $\theta_0 + \theta_1x$을 예측하려 한다.
이러한 직선을 찾는 것은 Squared Residuals (RSS)의 합을 최소화 시키는 것으로 구할 수 있다.
$$ RSS = \sum^n_{i=1}(y_i-\hat{y}_i)^2 = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 $$
어떻게 RSS를 최소화 시키는 $\boldsymbol{\theta} = [\theta_0 \theta_1]^T$를 찾을 수 있을까?
$$ RSS = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 $$
$$ \frac{\partial RSS}{\partial \theta_0} = \sum^n_{i=1}-2(y_i-(\theta_0+\theta_1x_i)) = 0 \Rightarrow n\theta_0 = \sum^n_{i=1}(y_i-\theta_1x_i) $$
$$ \Rightarrow \theta_0 = \bar{y}-\theta_1\bar{x} $$
$$ RSS = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 = \sum^n_{i=1}(y_i-(\bar{y} - \theta_1\bar{x})-(\theta_1x_i))^2 $$
$$ = \sum^n_{i=1}(y_i-\bar{y}-\theta_1(x_i-\bar{x}))^2 $$
$$ \frac{\partial RSS}{\partial \theta_1} = \sum^n_{i=1} -2(y_i-\bar{y}-\theta_1(x_i-\bar{x}))(x_i-\bar{x}) = 0 $$
$$ \Rightarrow \theta_1 = \frac{\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}{\sum^n_{i=1}(x_i-\bar{x})^2} $$
Multivariate Linear Regression
이번엔 3차원 이상에서 존재하는 data point를 상상해보자.
예를 들면 집의 가격, 집에 존재하는 방의 갯수, 집의 넓이를 포함한 data points를 생각해보자.
먼저, multidimension의 형태를 갖고 있는 vector $\boldsymbol{x} = (x_1, x_2, ..., x_p)$를 생각해보자, 그것의 linear predictor는 다음과 같이 정의된다: $y = \theta_0 + \theta_1x_1 + ... + \theta_px_p + \epsilon$
이것은 linear 형태로 작성될 수 있다:
$$y = <\boldsymbol{\theta}, \boldsymbol{x}> + \epsilon$$
$$\Rightarrow y = \boldsymbol{\theta}^T\boldsymbol{x} + \epsilon$$
이 때, $$\boldsymbol{\theta} = \begin{pmatrix} \theta_0 \\ \theta_1 \\ ... \\ \theta_p \end{pmatrix} , \boldsymbol{x} = \begin{pmatrix} 1 \\ x_1 \\ ... \\ x_p \end{pmatrix} $$
그렇다면 전체 dataset $D = { (x_1,y_1), ... , (x_n, y_n)}$에 대해서 예측해보자.
우리는 $ ||\boldsymbol{y}-\boldsymbol{\hat{y}}||^2_2 = ||\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\theta}||^2_2 $를 최소화하는 $\boldsymbol{\theta}$를 찾고 싶다.
$$\boldsymbol{\theta}^{OLS} = min_{\boldsymbol{\theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2_2 $$
$$||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 = <\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta},\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}>$$
$$\frac{\partial (...)}{\partial \boldsymbol{\theta}} = 2<-\boldsymbol{X}, \boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}> = -2(\boldsymbol{X}^T\boldsymbol{y} - \boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta}) = 0 $$
$$\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta} = \boldsymbol{X}^T\boldsymbol{y} \text{(normal equation)} $$
$$ \boldsymbol{\theta} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} $$
하지만 matrix inverse를 이용하여 normal equation을 푸는 행동의 cost는 매우 높다는 것을 명심해야한다.
그렇기에 normal equation $\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\hat{\theta}} = \boldsymbol{X}^T\boldsymbol{y}$를 푸는 방법에는 여러가지가 있다.
1. Cholesky decomposition (factorization) - 빠르지만, rounding error에 매우 민감하다.
2. QR decomposition (factorization) - 안정적이고 상대적으로 빠르다.
3. SVD (Singular Vector Decomposition) - 매우 안정적이다.
Probabilistic Interpretation
다음과 같은 linear regressor를 고려해보자: $y_i = <\boldsymbol{\theta}, \boldsymbol{x}_i> + \epsilon_i$
이 때, noise $\epsilon_i$에 대하여, 가우스 분포를 따른다고 가정하자. $\epsilon_i \sim N(0, \sigma^2)$
그렇다면, $\epsilon_i$에 대하여, density는 다음과 같다: $p(\epsilon_i) = \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{\epsilon^2_i}{2\sigma^2})$
이것은 다음을 의미한다 : $p(y_i|\boldsymbol{x}_i;\boldsymbol{\theta}) = \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2})$
그렇다면, 우리는 $y_i$에 대한 분포를 찾아야 한다.
likehood function으로서, $\boldsymbol{\theta}$값의 함수를 생각해보자.
$$L(\boldsymbol{\theta}) = L(\boldsymbol{\theta};\boldsymbol{X},\boldsymbol{y}) = p(\boldsymbol{y}|\boldsymbol{X};\boldsymbol{\theta}).$$
$\epsilon_i$에 대한 독립 가정을 세우면, 다음과 같이 정리할 수 있다.
$$L(\boldsymbol{\theta}) = \prod^n_{i=1}p(y_i|\boldsymbol{x}_i;\boldsymbol{\theta}) = \prod^n_{i=1} \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2})$$
우리는 주어진 확률 모델에서 likelihood function을 최대화하는 $\boldsymbol{\theta}$를 찾는 것이 목표이다. - maximum likelihood estimator
이 likelihood function에 log를 뒤집혀 씌우면 이를 log likelihood라 한다.
$$ l(\boldsymbol{\theta}) = log L(\boldsymbol{\theta}) = log \prod^m_{i=1} \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{theta})^2}{2\sigma^2}) $$
$$ =\sum^m_{i=1}log\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2}) $$
$$ =mlog\frac{1}{\sqrt{2\pi\sigma}} - \frac{1}{\sigma^2}\cdot\frac{1}{2}\sum^m_{i=1}(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2 $$
그러므로 $l(\boldsymbol{\theta})$를 최대화 시키는 것은 $\sum^m_{i=1}(y_i-\boldsymbol{x}\boldsymbol{\theta})^2 = ||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2$의 답과 똑같이 된다.
Ridge Regression
Linear regression with L2-regularization
$$ \hat{\boldsymbol{\theta}}^{ridge} = \min_{\boldsymbol{theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$ \text{As } \lambda \rightarrow 0, \hat{\boldsymbol{\theta}}^{ridge} = \hat{\boldsymbol{\theta}}^{OLS} $$
Ridge regression을 분석해보자.
$$\hat{\boldsymbol{\theta}}^{ridge} = \min_{\boldsymbol{\theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$PRSS(\boldsymbol{\theta})_{l2} = ||\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$ \frac{\partial PRSS(\boldsymbol{\theta})_{l2}}{\partial \boldsymbol{\theta}} = -2(\boldsymbol{X}^T\boldsymbol{y} - \boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta}) + 2\lambda\boldsymbol{\theta} = 0 $$
$$ \hat{\boldsymbol{\theta}}^{ridge} = (\boldsymbol{X}^T\boldsymbol{X} + \lambda{\boldsymbol{I}}_p)^{-1}\boldsymbol{X}^T\boldsymbol{y} $$
이 때, $\boldsymbol{X}$는 standardized, $\boldsymbol{y}$는 center되어 있다.
Hyperparameters
대부분의 머신 러닝 알고리즘은 학습 알고리즘을 조절할 수 있게 하는 몇 가지 세팅 장치가 있는데, 이들을 hyperpameter라 부르며, 이들은 학습되지 않는다.
예를 들면 L2-regularization term에서 $\lambda$와 같은 녀석들이 되겠다.
하지만 때때로 최적화된 hyperpameter를 찾긴 힘들어서 이들을 설정할 때 주의하여야 한다.
이러한 hyperparameter는 보통 여러번의 validation을 통해 도출하기도 한다.
Cross Validation
예를 들어 learning step이 매우 많을 경우에 training set에 한정해서는 좋은 performance를 보여줄 수 있지만, test set에서는 나쁜 performance를 보여줄 수 있다. 이러한 learning step과 같은 hyperparameter를 조정하기 위해서는 training 단계에서 관찰되지 않는 example들을 포함한 validation set을 이용한 validation step이 필요하다. 이 일정 학습 반복 단계마다 validation으로 performance가 어느 정도 되는지 보여주며 현재 training이 잘 되어가고 있는지, overfitting이 되어가고 있는지에 대해서 보여주는 set라 생각하면 된다.
하지만, 이러한 training에서 training set의 크기가 큰 영향을 끼치는 만큼 validation set을 잘라내는 일은 가슴 아프다.
그래서 validation을 행할 때에는, 대부분 cross-validation을 이용하여 검증한다.
다음과 같이 Training Set에서 Data들을 n등분한다음, 하나의 모델에 대하여 오른쪽 그림과 같이 validation을 하는 것이다. 오른쪽 그림에서 나온 각각 Data의 validation performance를 통하여 모델을 검증한다.
아래의 설명은 k-Fold Cross Validation에 대한 자세한 설명이다.
다음 편에서는 Classification, k-NN, Logistic Regression, Sigmoid Function과 같은 내용을 다뤄보도록 하겠다.
Point Estimation
Point estimation은 우리가 관심있는 것들에 대한 단일 최고의 예측을 제공하려는 시도 중에 하나이다.
예를 들어서, ${x^{(1)}, ... , x^{(m)}}$이 data point $m$개의 세트라고 하면, 포인트 추정자(point estimator)는 data에 관한 어느 함수로 정의된다:
$$ \hat{\theta_m} = h(x^{(1)}, ... , x^{(m)}). $$
물론 이러한 정의에서는 $h$ 함수 자체가 참 $\theta$값에 가까운 값을 요구하지도 않기 때문에 어느 함수라도 추정자로서 적합하지만, 물론 좋은 추정자는 참 $\theta$값을 생성하는 함수이겠다.
그렇다면, 통계적 관점을 집어넣는다면 어떻게 될까.
먼저 앞에서 언급한 부분을 생각하면, 실제 매개 변수 값 $\theta$는 고정되어 있지만 우리가 모르는 값이며, 점 추정치(point estimate) $\theta$는 데이터의 함수이다.
Data가 무작위적 과정을 거쳐 뽑아나왔고, data의 함수도 무작위이기 때문에 $\hat{\theta}$도 무작위적 과정이다.
점 추정은 또한 input과 target variable의 추정을 참조하기도 한다.
우리는 함수 추정자로써 점 추정의 이러한 형태들을 취하기도 한다.
Function Estimation
주어진 input vector x에 대하여 변수 y를 예측한다고 상상하자.
우리는 y와 x에 관한 대략적인 관계를 묘사하는 참 함수 $f(x)$가 존재한다고 가정한다.
(e.g.) 우리는 $y = f(x) + \epsilon$과 같은 식을 상상할 수 있고, 이 때 $\epsilon$은 x로부터 예측되지 않은 y의 부분값이다.
함수 추정에서 우리는 추정자 h에 대해 f를 근사시키고 싶어한다.
Bias
추정자의 Bias는 다음과 같이 정의된다.
$$bias(\hat{\theta}_m) = E(\hat{\theta}_m) - \theta$$
이 때, $\theta$는 데이터 생성 분포를 정의하는 데 사용되는 $\theta$의 실제 기본값이다.
만약 $bias(\hat{\theta}_m)=0$이면, $E((\hat{\theta}_m)) = \theta$이므로, 추정치$\hat{\theta}_m$가 비편향 (unbiased)됐다고 하며,
만약 $\lim_{m->\infty}bias(\hat{\theta}_m)=0$일 경우, $\lim_{m->\infty}E(\hat{\theta}_m) = \theta$이므로 $\hat{\theta}_m$가 asymptotically unbiased됐다고 한다.
이러한 식으로보면 잘 이해가 안 되니까 예시를 들어서 살펴보도록 하자.
먼저 data sample $\{x^{(1)}, ... x^{(m)}\}$에 대해 모두 독립적이고 이상적으로 베르누어 분포를 따른다고하자. 즉 data sample들이 Bernoulli distribution으로부터 비롯됐다고 가정하자. 이 때, 평균을 $\theta$라 하면,
$$P(x^{(i)};\theta) = \theta^{x^{(i)}}(1-\theta)^{(1-x^{(i)})}$$
분포 \theta 파라미터에 대한 일반적인 추정치는 training sample의 평균이다:
$$\hat{\theta}_m = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$
그렇다면 이러한 추정치가 편향되어 있는지 편향되지 않았는지 확인해보자.
$$ bias(\hat{\theta}_m) = E[\hat{\theta}_m] - \theta $$
$$ = E[\frac{1}{m}\sum^m_{i=1} x^{(i)}] - \theta = \frac{1}{m}\sum^m_{i=1}E[x^{(i)}] - \theta $$
$$ = \frac{1}{m}\sum^m_{i=1}\sum^1_{x^{(i)}=0}(x^{(i)}\theta^{x^{(i)}}(1-\theta)^{(1-x^{(i)})}) - \theta $$
$$ = \frac{1}{m}\sum^m_{i=1}(\theta) - \theta = \theta - \theta = 0 $$
따라서 $$\hat{\theta}_m = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$는 편향되지 않았다.
그렇다면 편향되어있는 추정치의 예시에는 뭐가 있을까.
Gaussian distribution의 Variance parameter $\sigma^2$에 대해 생각해보자.
샘플 Variance는 하나의 추정치로써 다음과 같이 정의될 수 있다:
$$\hat{\sigma}^2_m = \frac{1}{m}\sum^m_{i=1}(x^{(i)} - \hat{\mu}_m)^2$$
그럴 경우, 이 추정치의 bias는
$$ bias(\hat{\sigma}^2_m) = E[\hat{\sigma}^2_m] - \sigma^2 = E[\frac{1}{m}\sum^m_{i=1}(x^{(i)}- \hat{\mu}_m)^2] - \sigma^2 = \frac{m-1}{m}\sigma^2 - \sigma^2 = - \frac{\sigma^2}{m} $$
따라서 sample variance는 편향적이다.
정리해보면 Discrepancy들은 다음과 같다.
Bias
$$ Bias[h(x)] = \bar{h(x)} - f(x) $$
Variance
$$ Var[h(x)] = E_p[(h(x)-\bar{h(x)})^2] $$
Noise
$$ Noise[h(x)] = E[(y-f(x))^2] = E[\epsilon^2] = \sigma^2 $$
Bias-Variance Decomposition
우리는 variance lemma을 통해 기대되는 예측 에러값을 분해할 수 있다.
$$E[(y-h(x))^2] = E[h(x)^2 - 2yh(x) + y^2] = E[h(x)^2] + E[y^2] - 2E[y]E[h(x)]$$
x에 대한 가설의 평균 예측을 $\bar{h(x)} = E[h(x)]$라 하자.
첫 번째 term은 variance lemma $E[X^2] = Var[X] + bar{X}^2$에 의해 다음과 같이 분해될 수 있다.
$$E[h(x)^2] = E[(h(x)-\bar{h(x)})^2] + \bar{h(x)}^2$$
두 번째 term은 다음과 같이 분해될 수 있다.
$$E[y^2] = E[(y-f(x))^2] + f(x)^2$$
그렇다면 이러한 식을 한꺼번에 모아두자.
$$E[(y-h(x))^2]$$
$$=E[h(x)^2-2yh(x)+y^2] $$
$$=E[h(x)^2]+E[y^2]-2E[y]E[h(x)]$$
$$=E[(h(x)-\bar{h(x)})^2] + \bar{h(x)}^2 + E[(y-f(x))^2] + f(x)^2 - 2f(x)\bar{h(x)} $$
$$=E[(h(x)-\bar{h(x)})^2] + (\bar{h(x)}-f(x))^2 + E[(y-f(x))^2] $$
$$=Var + Bias^2 + Noise $$
위와 같은 그림에서 왼쪽 그림은 높은 Bias를 가지고 있지만 낮은 Variance를 가지고 있다, 하지만 오른쪽 그림에서는 낮은 Bias를 가지고 있지만 높은 Variance를 가지고 있다.
우리는 그림과 같이 Bias와 Variance 모두가 적절하게 낮은 Optimal Capacity를 찾는 것이 목표이다.
Linear Regression
우리는 집의 가격과 그 집의 넓이에 관한 데이터를 가지고 있다고 생각하자.
우리는 이러한 데이터 포인트들에 대하여 직선 $\theta_0 + \theta_1x$을 예측하려 한다.
이러한 직선을 찾는 것은 Squared Residuals (RSS)의 합을 최소화 시키는 것으로 구할 수 있다.
$$ RSS = \sum^n_{i=1}(y_i-\hat{y}_i)^2 = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 $$
어떻게 RSS를 최소화 시키는 $\boldsymbol{\theta} = [\theta_0 \theta_1]^T$를 찾을 수 있을까?
$$ RSS = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 $$
$$ \frac{\partial RSS}{\partial \theta_0} = \sum^n_{i=1}-2(y_i-(\theta_0+\theta_1x_i)) = 0 \Rightarrow n\theta_0 = \sum^n_{i=1}(y_i-\theta_1x_i) $$
$$ \Rightarrow \theta_0 = \bar{y}-\theta_1\bar{x} $$
$$ RSS = \sum^n_{i=1}(y_i-(\theta_0 + \theta_1x_i))^2 = \sum^n_{i=1}(y_i-(\bar{y} - \theta_1\bar{x})-(\theta_1x_i))^2 $$
$$ = \sum^n_{i=1}(y_i-\bar{y}-\theta_1(x_i-\bar{x}))^2 $$
$$ \frac{\partial RSS}{\partial \theta_1} = \sum^n_{i=1} -2(y_i-\bar{y}-\theta_1(x_i-\bar{x}))(x_i-\bar{x}) = 0 $$
$$ \Rightarrow \theta_1 = \frac{\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}{\sum^n_{i=1}(x_i-\bar{x})^2} $$
Multivariate Linear Regression
이번엔 3차원 이상에서 존재하는 data point를 상상해보자.
예를 들면 집의 가격, 집에 존재하는 방의 갯수, 집의 넓이를 포함한 data points를 생각해보자.
먼저, multidimension의 형태를 갖고 있는 vector $\boldsymbol{x} = (x_1, x_2, ..., x_p)$를 생각해보자, 그것의 linear predictor는 다음과 같이 정의된다: $y = \theta_0 + \theta_1x_1 + ... + \theta_px_p + \epsilon$
이것은 linear 형태로 작성될 수 있다:
$$y = <\boldsymbol{\theta}, \boldsymbol{x}> + \epsilon$$
$$\Rightarrow y = \boldsymbol{\theta}^T\boldsymbol{x} + \epsilon$$
이 때, $$\boldsymbol{\theta} = \begin{pmatrix} \theta_0 \\ \theta_1 \\ ... \\ \theta_p \end{pmatrix} , \boldsymbol{x} = \begin{pmatrix} 1 \\ x_1 \\ ... \\ x_p \end{pmatrix} $$
그렇다면 전체 dataset $D = { (x_1,y_1), ... , (x_n, y_n)}$에 대해서 예측해보자.
우리는 $ ||\boldsymbol{y}-\boldsymbol{\hat{y}}||^2_2 = ||\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\theta}||^2_2 $를 최소화하는 $\boldsymbol{\theta}$를 찾고 싶다.
$$\boldsymbol{\theta}^{OLS} = min_{\boldsymbol{\theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2_2 $$
$$||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 = <\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta},\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}>$$
$$\frac{\partial (...)}{\partial \boldsymbol{\theta}} = 2<-\boldsymbol{X}, \boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}> = -2(\boldsymbol{X}^T\boldsymbol{y} - \boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta}) = 0 $$
$$\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta} = \boldsymbol{X}^T\boldsymbol{y} \text{(normal equation)} $$
$$ \boldsymbol{\theta} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} $$
하지만 matrix inverse를 이용하여 normal equation을 푸는 행동의 cost는 매우 높다는 것을 명심해야한다.
그렇기에 normal equation $\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\hat{\theta}} = \boldsymbol{X}^T\boldsymbol{y}$를 푸는 방법에는 여러가지가 있다.
1. Cholesky decomposition (factorization) - 빠르지만, rounding error에 매우 민감하다.
2. QR decomposition (factorization) - 안정적이고 상대적으로 빠르다.
3. SVD (Singular Vector Decomposition) - 매우 안정적이다.
Probabilistic Interpretation
다음과 같은 linear regressor를 고려해보자: $y_i = <\boldsymbol{\theta}, \boldsymbol{x}_i> + \epsilon_i$
이 때, noise $\epsilon_i$에 대하여, 가우스 분포를 따른다고 가정하자. $\epsilon_i \sim N(0, \sigma^2)$
그렇다면, $\epsilon_i$에 대하여, density는 다음과 같다: $p(\epsilon_i) = \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{\epsilon^2_i}{2\sigma^2})$
이것은 다음을 의미한다 : $p(y_i|\boldsymbol{x}_i;\boldsymbol{\theta}) = \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2})$
그렇다면, 우리는 $y_i$에 대한 분포를 찾아야 한다.
likehood function으로서, $\boldsymbol{\theta}$값의 함수를 생각해보자.
$$L(\boldsymbol{\theta}) = L(\boldsymbol{\theta};\boldsymbol{X},\boldsymbol{y}) = p(\boldsymbol{y}|\boldsymbol{X};\boldsymbol{\theta}).$$
$\epsilon_i$에 대한 독립 가정을 세우면, 다음과 같이 정리할 수 있다.
$$L(\boldsymbol{\theta}) = \prod^n_{i=1}p(y_i|\boldsymbol{x}_i;\boldsymbol{\theta}) = \prod^n_{i=1} \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2})$$
우리는 주어진 확률 모델에서 likelihood function을 최대화하는 $\boldsymbol{\theta}$를 찾는 것이 목표이다. - maximum likelihood estimator
이 likelihood function에 log를 뒤집혀 씌우면 이를 log likelihood라 한다.
$$ l(\boldsymbol{\theta}) = log L(\boldsymbol{\theta}) = log \prod^m_{i=1} \frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{theta})^2}{2\sigma^2}) $$
$$ =\sum^m_{i=1}log\frac{1}{\sqrt{2\pi\sigma}}exp(-\frac{(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2}{2\sigma^2}) $$
$$ =mlog\frac{1}{\sqrt{2\pi\sigma}} - \frac{1}{\sigma^2}\cdot\frac{1}{2}\sum^m_{i=1}(y_i-\boldsymbol{x}_i\boldsymbol{\theta})^2 $$
그러므로 $l(\boldsymbol{\theta})$를 최대화 시키는 것은 $\sum^m_{i=1}(y_i-\boldsymbol{x}\boldsymbol{\theta})^2 = ||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2$의 답과 똑같이 된다.
Ridge Regression
Linear regression with L2-regularization
$$ \hat{\boldsymbol{\theta}}^{ridge} = \min_{\boldsymbol{theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$ \text{As } \lambda \rightarrow 0, \hat{\boldsymbol{\theta}}^{ridge} = \hat{\boldsymbol{\theta}}^{OLS} $$
Ridge regression을 분석해보자.
$$\hat{\boldsymbol{\theta}}^{ridge} = \min_{\boldsymbol{\theta}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$PRSS(\boldsymbol{\theta})_{l2} = ||\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\theta}||^2 + \lambda||\boldsymbol{\theta}||^2_2 $$
$$ \frac{\partial PRSS(\boldsymbol{\theta})_{l2}}{\partial \boldsymbol{\theta}} = -2(\boldsymbol{X}^T\boldsymbol{y} - \boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\theta}) + 2\lambda\boldsymbol{\theta} = 0 $$
$$ \hat{\boldsymbol{\theta}}^{ridge} = (\boldsymbol{X}^T\boldsymbol{X} + \lambda{\boldsymbol{I}}_p)^{-1}\boldsymbol{X}^T\boldsymbol{y} $$
이 때, $\boldsymbol{X}$는 standardized, $\boldsymbol{y}$는 center되어 있다.
Hyperparameters
대부분의 머신 러닝 알고리즘은 학습 알고리즘을 조절할 수 있게 하는 몇 가지 세팅 장치가 있는데, 이들을 hyperpameter라 부르며, 이들은 학습되지 않는다.
예를 들면 L2-regularization term에서 $\lambda$와 같은 녀석들이 되겠다.
하지만 때때로 최적화된 hyperpameter를 찾긴 힘들어서 이들을 설정할 때 주의하여야 한다.
이러한 hyperparameter는 보통 여러번의 validation을 통해 도출하기도 한다.
Cross Validation
예를 들어 learning step이 매우 많을 경우에 training set에 한정해서는 좋은 performance를 보여줄 수 있지만, test set에서는 나쁜 performance를 보여줄 수 있다. 이러한 learning step과 같은 hyperparameter를 조정하기 위해서는 training 단계에서 관찰되지 않는 example들을 포함한 validation set을 이용한 validation step이 필요하다. 이 일정 학습 반복 단계마다 validation으로 performance가 어느 정도 되는지 보여주며 현재 training이 잘 되어가고 있는지, overfitting이 되어가고 있는지에 대해서 보여주는 set라 생각하면 된다.
하지만, 이러한 training에서 training set의 크기가 큰 영향을 끼치는 만큼 validation set을 잘라내는 일은 가슴 아프다.
그래서 validation을 행할 때에는, 대부분 cross-validation을 이용하여 검증한다.
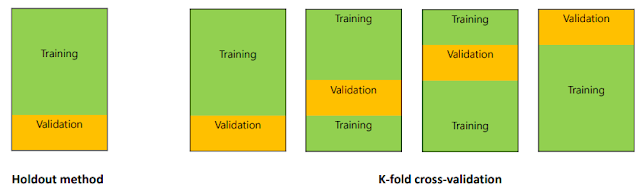
다음과 같이 Training Set에서 Data들을 n등분한다음, 하나의 모델에 대하여 오른쪽 그림과 같이 validation을 하는 것이다. 오른쪽 그림에서 나온 각각 Data의 validation performance를 통하여 모델을 검증한다.
아래의 설명은 k-Fold Cross Validation에 대한 자세한 설명이다.
k-Fold Cross Validation은 Train Dataset을 균등하게 k개의 그룹(Fold라고 합니다)으로 나누고 (k - 1)개의 Test Fold와 1개의 Validation Fold로 지정합니다. 그리고나서 총 k회 검증을 하는데, 각 검증마다 Test Fold를 다르게 지정하여 성능을 측정합니다. 이런 식으로 k회 검증이 완료되면 각 Hyperparameter에 대한 검증 결과를 평균을 내어 Hyperparameters를 튜닝합니다.
이 과정을 좀 더 자세하게 정리하면 다음과 같습니다:
- 전체 Dataset이 Train Dataset과 Test Dataset으로 주어집니다.
- Train Dataset을 나눌 k를 지정하고, 가급적 균등하게 그리고 랜덤으로 k개의 데이터 Fold로 나누되 (k - 1)개의 Fold는 Test용으로 1개는 Validation용으로 지정합니다.
- 튜닝하고자 하는 Hyperparameters를 정합니다.
- 정해진 Hyperparameters에 대하여 각각 검증하고자 하는 범위와 실험세트(요인 수준)를 정합니다.
- k개로 나누어진 Train Dataset 데이터 그룹에 대하여 서로 다른 Validation Fold를 지정하면서 아래의 오퍼레이션을 k번 반복합니다:· (k - 1)개의 Train Fold에 대하여 학습을 시킵니다.
· 나머지 1개의 Validation Fold에 대하여 성능을 측정합니다. 즉, 앞서 학습된 파라미터를 이용하여 Validation Fold를 이용하여 결과를 얻습니다. - 5번에서 얻은 각 Hyperparamer의 k개의 결과에 대한 평균을 계산하여 이 평균값을 각 Hyperaparameter로 지정합니다.
- 마지막으로, 6번에서 얻은 Hyperparameters를 적용하여 Test Data에 대하여 모델을 1회 평가합니다
출처: http://cinema4dr12.tistory.com/1275
다음 편에서는 Classification, k-NN, Logistic Regression, Sigmoid Function과 같은 내용을 다뤄보도록 하겠다.





댓글
댓글 쓰기