BOJ) 1014. 컨닝

문제:

최백준은 서강대학교에서 “컨닝의 기술”이라는 과목을 가르치고 있다. 이 과목은 상당히 까다롭기로 정평이 나있기 때문에, 몇몇 학생들은 시험을 보는 도중에 다른 사람의 답지를 베끼려 한다.

시험은 N행 * M열 크기의 직사각형 교실에서 이루어진다. 교실은 1*1 크기의 단위 정사각형으로 이루어져 있는데, 각 단위 정사각형은 자리 하나를 의미한다.

최백준은 컨닝을 방지하기 위해서 다음과 같은 전략을 세웠다. 모든 학생은 자신의 왼쪽, 오른쪽, 왼쪽 대각선 위, 오른쪽 대각선 위, 이렇게 총 네 자리에 앉아있는 친구의 답지를 항상 베낀다고 가정한다. 따라서, 자리 배치는 모든 학생이 컨닝을 할 수 없도록 배치되어야 한다.

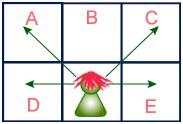
위의 그림을 보자. A , C , D 혹은 E에 다른 학생을 앉히는 것은 좋은 생각이 아니다. 그 이유는 이미 앉아있는 학생이 그들의 답안지를 베낄 우려가 있기 때문이다. 하지만, B에 다른 학생을 앉힌다면, 두 학생은 서로의 답지를 베낄 수 없어 컨닝의 우려가 없다.

위와 같이 컨닝이 불가능하도록 자리를 배치 하려는 최백준의 행동에 분노한 일부 학생들이 교실의 책상을 부셔버렸기 때문에, 일부 자리에는 학생이 앉을 수 없다.

최백준은 교실의 모양이 주어졌을 때, 이 곳에서 아무도 컨닝을 할 수 없도록 학생을 배치하였을 경우에 교실에 배치할 수 있는 최대 학생 수가 몇 명인지 궁금해졌다. 최백준을 위해 이를 구하는 프로그램을 작성하라.

https://www.acmicpc.net/problem/1014

해설:

bitmask dp로 풀 수 있다고는 하지만, 현재 필자가 network flow를 공부하는중 이므로 network flow를 이용한 해설을 적어보도록 하겠다.

먼저 잘 생각해보면 같은 열에 있는 자리는 절대로 컨닝할 수 없다.

즉 홀수열, 짝수열로 그래프를 나누면, 이분 그래프가 만들어진다는 것이다.

홀수열 짝수열로 그래프를 만든후 컨닝이 되는 자리들을 서로서로 연결하면, 

이분 그래프가 된다.

우리가 원하는 것은 시험을 볼 수 있는 최대 학생의 수다.

즉 이 edge들을 모두 cover하는 minimum vertex cover를 구한 후 전체 자리 수에서 빼주면 된다.

이분 그래프에서 minimum vertex cover는 maximum bipartite matching과 같으므로, 이분 매칭을 이용해서 풀어주자.

코드:

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <utility>
using namespace std;

int M, N;
bool visited[105];
bool map[105][105];
int aMatched[105], bMatched[105];
char arr[15][15];
pair<int, int> pleft[105];
pair<int, int> pright[105];

bool dfs(int p){
        if(visited[p]) return 0;
        visited[p] = 1;
        for(int i=0; i<N; i++){
                if( map[p][i] ){
                        if( bMatched[i] == -1 || dfs(bMatched[i]) ){
                                bMatched[i] = p;
                                aMatched[p] = i;
                                return 1;
                        }
                }
        }
        return 0;
}

int main(){
        int T; cin>>T;
        int dy[4] = {-1, -1, 1, 1};
        int dx[4] = {-1, 0, 0, -1};
        while(T--){
                memset(map,0,sizeof(map));
                M=0; N=0;
                int n, m;
                scanf("%d%d",&n,&m);
                for(int i=0; i<n; i++) scanf("%s",arr[i]);
                for(int i=0; i<m; i+=2){
                        for(int j=0; j<n; j++){
                                if(arr[j][i] == '.')
                                        pleft[M++] = make_pair(j,i);
                        }
                }
                for(int i=1; i<m; i+=2){
                        for(int j=0; j<n; j++){
                                if(arr[j][i] == '.')
                                        pright[N++] = make_pair(j,i);
                        }
                }
                for(int i=0; i<M; i++){
                        for(int j=0; j<N; j++){
                                int lx = pleft[i].first; int ly = pleft[i].second;
                                int rx = pright[j].first; int ry = pright[j].second;

                                for(int k=0; k<4; k++){
                                        if( lx+dx[k] == rx && ly+dy[k] == ry)  map[i][j] = 1;
                                        if( rx+dx[k] == lx && ry+dy[k] == ly)  map[i][j] = 1;
                                }
                        }
                }
                int size = 0;
                memset(bMatched,-1,sizeof(bMatched));
                for(int i=0; i<M; i++){
                        memset(visited,0,sizeof(visited));
                        size += dfs(i);
                }
                printf("%d\n",M+N-size);
        }
}